Parallélogramme
a) Triangle rectangle :
Un triangle rectangle est un triangle qui possède un angle droit.
Théorème de Pythagore
et sa réciproque : un triangle ABC est rectangle en A si et seulement si 
 |
Propriétés :
· Dans
un triangle rectangle, on note 
la mesure en degrés
de l’un des deux angles aigus. On a 
· Dans un triangle rectangle, les médiatrices des deux côtés adjacents à l’angle droit se coupent au milieu I de l’hypoténuse.
· Dans
un triangle rectangle ABC, rectangle en B, I est le milieu de 
. Les points A, B et C appartiennent au
cercle 
C de centre I et de
rayon AI. Le cercle C s’appelle cercle
circonscrit au triangle ABC. Si un triangle est inscrit dans un cercle et que
l’un de ses côtés est un diamètre de ce cercle, alors ce triangle est
rectangle .
 |
b) Triangle isocèle :
 |
Un triangle ABC est isocèle en A si AB = AC
Dans un triangle ABC isocèle en A :
· Les angles à la base
ont la même mesure : 
;
· Le
point H est le milieu du segment 
;
· La
droite (HA) est la médiatrice de 
, c’est l’axe de
symétrie du triangle et la bissectrice de l’angle 
Un triangle est rectangle isocèle en
A lorsque 
et AB = AC
c) Triangle équilatéral :
 |
· Un triangle ABC est équilatéral si AB = AC = BC ;
· Les trois angles d’un triangle équilatéral ont pour mesure 60° ;
· Un triangle équilatéral a trois axes de symétrie, qui sont les médiatrices des côtés, les hauteurs, les bissectrices des angles
2. Coordonnées de points du plan :
a) Repères :
 |
Définition :
Un repère orthonormal d’origine le point O, est un triplet (O;I;J ) de points tels que le triangle OIJ est rectangle isocèle en O.
La droite graduée (O;I) du repère est l’axe des abscisses.
La droite graduée (O;J) du repère est l’axe des ordonnées.
Remarque :
Le repère (O;I;J ) est dit orthogonal lorsque le triangle OIJ est rectangle en O.
Pour certains repères (O ;I;J ), le triangle OIJ n’est pas rectangle.
 |
Coordonnées de points :
Propriété :
Tout
point M est repéré par un unique couple 
de nombres réels appelé coordonnées
du point M.
est l’abscisse de M et 
est l’ordonnée de M.
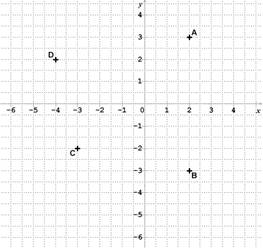
Exemple 1 : Exemple 2 :
| Les points A, B, C et D sont placés sur un repère orthonormé. Déterminer les coordonnées de ces points | Placer dans le repère ci-dessous les points
|
||||||||||||||
|
|
|
||||||||||||||
|
b) Milieu d’un segment :
Propriété :
Dans un repère
orthonormé, 
sont deux points.
Le milieu I du segment 
a pour coordonnées 
.
Exemple 3 :
Le point I est le
milieu du segment . Compléter le
tableau en calculant les coordonnées des points A, B ou I.
| A |
|
|
|
|
|
|
| B |
|
|
|
|
|
|
| I |
|
|
|
|
|
|
c) Distance entre deux points :
Propriété :
Dans un repère
orthonormé, 
sont deux points.
La distance entre les
points A et B est :
3. Les quadrilatères :
a) Parallélogramme
Définition :
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles deux à deux
Propriétés :
· Le point d’intersection des diagonales est un centre de symétrie du parallélogramme.
b) Rectangle
Définition :
Un rectangle est un quadrilatère qui a quatre angles droits.
Propriétés :
· Un quadrilatère est un rectangle si, et seulement si, ses diagonales se coupent en leur milieu et ont la même longueur.
· Un parallélogramme qui a un angle droit est un rectangle.
c) Losange
 |
Définition :
Un losange est un quadrilatère qui a quatre côtés de même longueur.
Propriétés :
· Un quadrilatère est un losange si, et seulement si, ses diagonales sont perpendiculaires en leur milieu.
· Un parallélogramme qui deux côtés consécutifs de même longueur est un losange.
d) Carré
 |
Définition :
Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur.
Remarque : Un carré est à la fois un rectangle et un losange.
4. Tangente à un cercle :
Définition :
C est un cercle de centre O et A est un point
de ce cercle. La tangente au cercle C en A est la droite perpendiculaire en A à la
droite (OA).
 |
A
C
O
La droite (d) est la tangente en A au cercle C
(d)